Vectors in 2D and 3D - Mohsen Hamedi

Notation and Terminology

In a $\overrightarrow{AB}$ vector, $A$ is the start point and $B$ is the endpoint. And, the magnitude of such a vector is $|| \overrightarrow{AB} ||$ . Equal vectors have the same direction and magnitude.
The negative of a vector, $- \overrightarrow{AB}$ , has the same magnitude, but in the opposite direction of $\overrightarrow{AB}$ .

Addition and Subtraction

To add vectors in a coordinate plane, we have:

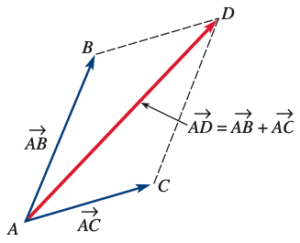
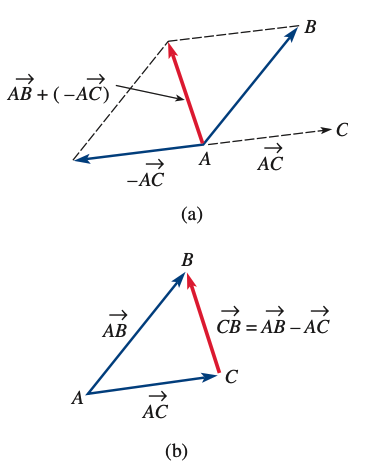
(1) $\begin{equation*}\boldsymbol{AD} = \boldsymbol{AB} + \boldsymbol{AC} = ~ < AB_1 + AC_1 , ~ AB_2 + AC_2 > .\end{equation*}$

And the subtraction of two vectors is

(2) $\begin{equation*}\boldsymbol{AB} - \boldsymbol{AC} = ~ < AB_1 - AC_1 , AB_2 - AC_2 >.\end{equation*}$

This is equivalent to

(3) $\begin{equation*}\boldsymbol{AB} - \boldsymbol{AC} = \boldsymbol{AB} + (- \boldsymbol{AC}),\end{equation*}$

which is depicted in figure a.

Magnitude of a Vector

The magnitude, length, or norm of a vector is

(4) $\begin{equation*} || \boldsymbol{a} || = \sqrt{a_1^2 + a_2^2}. \end{equation*}$

A unit vector, is a vector that has a magnitude of $1$ .

Normalization of a Vector

The normalized vector of $\boldsymbol{a}$ is a unit vector in the same direction as $\boldsymbol{a}$ . This means that a non-zero vector $\boldsymbol{a}$ is normalized as follows

(5) $\begin{equation*}\boldsymbol{u} = \frac{\boldsymbol{a}}{|| \boldsymbol{a} ||},\end{equation*}$

where $\boldsymbol{u}$ is the normalized vector of $\boldsymbol{a}$ .

The Unit Vectors in 2 Dimensions

The unit vectors $< 1,0 >$ and $< 0,1 >$ are known as the $\boldsymbol{i}$ and $\boldsymbol{j}$ vectors, respectively.
In $R^2$ space, $a_1$ and $a_2$ are the horizontal and vertical components of $\boldsymbol{a}$ , respectively.

The Unit Vectors in 3 Dimensions

The unit vectors $< 1,0,0 >, ~< 0,1,0 >$ , and $< 0,0,1 >$ are known as the $\boldsymbol{i} ,~ \boldsymbol{j}$ , and $\boldsymbol{k}$ vectors, respectively.

The Distance Between Two Points

The distance between $P_1(x_1,y_1,z_1)$ and $P_2(x_2,y_2,z_2)$ in 3-space is

(6) $\begin{equation*}d(P_1,P_2) = \sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 } .\end{equation*}$

Midpoint Formula

The midpoint of line segment between points $P_1$ and $P_2$ is

(7) $\begin{equation*}\left( \frac{x_1 + x_2}{2} , \frac{y_1 + y_2}{2} , \frac{z_1 + z_2}{2} \right) .\end{equation*}$

Vectors in 3-Space

Similar to $R^2$ space, vectors are defined in $R^3$ space as $\boldsymbol{a} = ~ < a_1, a_2, a_3 >$ .

Reference

Dennis G. Zill. Advanced Engineering Mathematics, $6^{th}$ edition. Jones $\&$ Bartlett Learning. 2016.