The Layers of the Atmosphere
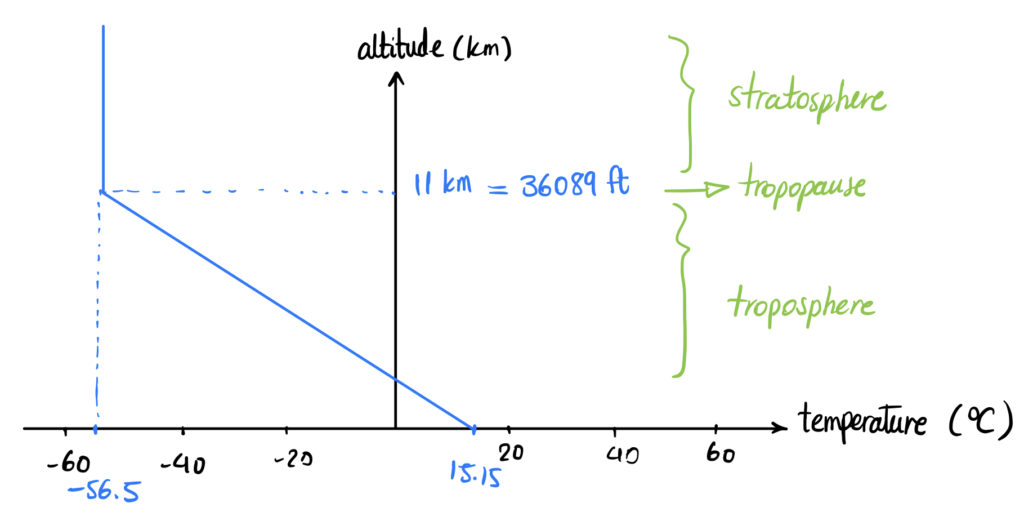
The first two major layers of the atmosphere are the troposphere and the stratosphere. These two layers, along with the temperature variations across them are depicted below. The temperature drops in the troposphere at a constant rate, by increasing the altitude, and it reaches a constant value at the tropopause and remains constant in the stratosphere.
To learn more about the different layers in the atmosphere, visit this webpage from NASA.
Temperature Variation in the Standard Atmosphere
Temperature decreases with increasing altitude. The rate is ![]() , or
, or ![]() , up to the tropopause. From the tropopause upward, temperature remains at a constant value of
, up to the tropopause. From the tropopause upward, temperature remains at a constant value of ![]() . Note that, the standard temperature at mean sea level is
. Note that, the standard temperature at mean sea level is ![]() . Thus, the standard temperature at a given altitude is
. Thus, the standard temperature at a given altitude is
(1) ![]()
where
Pressure Variation in the Standard Atmosphere
Pressure at sea level is ![]() , where
, where ![]() is hectoPascal and
is hectoPascal and ![]() . Pressure above the sea level and below the tropopause is obtained using the following equation:
. Pressure above the sea level and below the tropopause is obtained using the following equation:
(2) ![]()
where
Furthermore, the pressure above the tropopause is obtained via
(3) ![]()
where
Density Variation in the Standard Atmosphere
Density is always
(4) ![]()
where
Temperature, Pressure, and Density Ratios
The temperature, pressure, and density ratios are defind as
(5) ![]()
(6) ![]()
(7) ![]()
respectively.
Temperature, Pressure, and Density Ratios Variations
Below the tropopause
(8) ![]()
(9) ![]()
(10) ![]()
Above the tropopause
(11) ![]()
(12) ![]()
(13) ![]()
where