4.1 Complex Number
4.1.1 Definition
Any number of the form ![]() is called a complex number, where
is called a complex number, where ![]() and
and ![]() are real numbers and
are real numbers and ![]() is the imaginary unit.
is the imaginary unit.
The real part of the complex number, ![]() , is
, is ![]() , and
, and ![]() is the imaginary part of
is the imaginary part of ![]() .
.
4.1.2 Arithmetic Operations
Addition
(1) ![]()
Subtraction
(2) ![]()
Multiplication
(3) ![]()
Division
(4) ![]()
4.1.3 Conjugate
If ![]() is a complex number, then the complex conjugate, or simply the conjugate, of
is a complex number, then the complex conjugate, or simply the conjugate, of ![]() is
is
(5) ![]()
The arithmetic operations of a conjugate are as follows
(6) ![]()
4.1.4 Modulus or Absolute Value
The absolute value of ![]() is defined as
is defined as
(7) ![]()
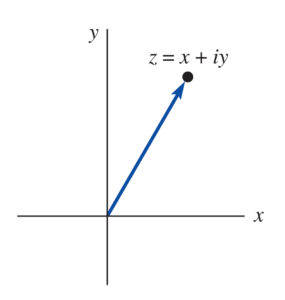
4.1.5 Geometric Interpretation
The following coordinate plane is known as the complex plane or simply the z-plane. The ![]() -axis is the real axis, and the
-axis is the real axis, and the ![]() -axis is the imaginary axis. The absolute value of a complex number is the distance of that number to the origin.
-axis is the imaginary axis. The absolute value of a complex number is the distance of that number to the origin.
4.2 Powers and Roots
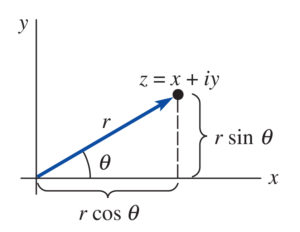
4.2.1 Polar Form
The polar form of a complex number, ![]() , is
, is
(8) ![]()
4.2.2 DeMoivre’s Formula
(9) ![]()
4.2.3 Integers Powers of 
The integer powers of a complex number can be found easily by applying the DeMoivre’s formula on the polar form of ![]() as follows
as follows
(10) ![]()
(11) ![]()
(12) ![]()
4.2.4 Roots of 
A number ![]() is the
is the ![]() root of a complex number
root of a complex number ![]() , if
, if ![]() .
.
Let’s assume that ![]() , then we can find the values of
, then we can find the values of ![]() and
and ![]() as follows
as follows
(13) ![]()
(14) ![]()
So,
(15) ![]()
By summarizing the results, the
(16) ![]()
4.3 Problems
Reference
Dennis G. Zill. Advanced Engineering Mathematics, ![]() edition. Jones
edition. Jones ![]() Bartlett Learning. 2016.
Bartlett Learning. 2016.
