Notation and Terminology
In a ![]() vector,
vector, ![]() is the start point and
is the start point and ![]() is the endpoint. And, the magnitude of such a vector is
is the endpoint. And, the magnitude of such a vector is ![]() . Equal vectors have the same direction and magnitude.
. Equal vectors have the same direction and magnitude.
The negative of a vector, ![]() , has the same magnitude, but in the opposite direction of
, has the same magnitude, but in the opposite direction of ![]() .
.
Addition and Subtraction
To add vectors in a coordinate plane, we have:
(1) ![]()
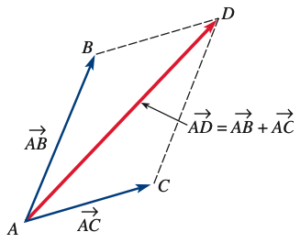
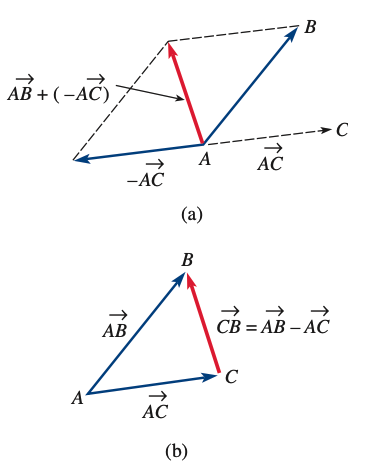
And the subtraction of two vectors is
(2) ![]()
This is equivalent to
(3) ![]()
which is depicted in figure a.
Magnitude of a Vector
The magnitude, length, or norm of a vector is
(4) ![]()
A unit vector, is a vector that has a magnitude of
Normalization of a Vector
The normalized vector of ![]() is a unit vector in the same direction as
is a unit vector in the same direction as ![]() . This means that a non-zero vector
. This means that a non-zero vector ![]() is normalized as follows
is normalized as follows
(5) ![]()
where
The Unit Vectors in 2 Dimensions
The unit vectors ![]() and
and ![]() are known as the
are known as the ![]() and
and ![]() vectors, respectively.
vectors, respectively.
In ![]() space,
space, ![]() and
and ![]() are the horizontal and vertical components of
are the horizontal and vertical components of ![]() , respectively.
, respectively.
The Unit Vectors in 3 Dimensions
The unit vectors ![]() , and
, and ![]() are known as the
are known as the ![]() , and
, and ![]() vectors, respectively.
vectors, respectively.
The Distance Between Two Points
The distance between ![]() and
and ![]() in 3-space is
in 3-space is
(6) ![]()
Midpoint Formula
The midpoint of line segment between points ![]() and
and ![]() is
is
(7) ![]()
Vectors in 3-Space
Similar to ![]() space, vectors are defined in
space, vectors are defined in ![]() space as
space as ![]() .
.
Reference
Dennis G. Zill. Advanced Engineering Mathematics, ![]() edition. Jones
edition. Jones ![]() Bartlett Learning. 2016.
Bartlett Learning. 2016.
