2.1 Autonomous Differential Equation
2.1.1 Autonomous First-Order Differential Equation
In the autonomous DE, the independent variable does not appear in the equation explicitly. The general and normal forms of such equations are:
(1) ![]()
For the definitions of the general and normal forms of a differential equation, see the definitions in Chapter 1.
2.1.2 Critical Points of an Autonomous DE
The zeros of function ![]() in the above definition, are known as the critical points of an autonomous differential equation. These points are also known as equilibrium points or stationary points.
in the above definition, are known as the critical points of an autonomous differential equation. These points are also known as equilibrium points or stationary points.
2.1.3 Attractors and Repellers of an Autonomous Differential Equation
The order of a differential equation is the order of the highest derivative in the equation. A second-order PDE and a third-order ODE are shown below.
This is explained in details in the following video.
2.2 Separable Differential Equations
2.2.1 Separable First-Order Differential Equation
A separable differential equation has a general form of
(2) ![]()
This type of differential equations can be solved by separating the variables as follows
(3) ![]()
2.3 Linear Differential Equations
2.3.1 Linear First-Order Differential Equation
A linear differential equation in the dependent variable ![]() has a general form of
has a general form of
(4) ![]()
2.3.2 Homogeneous and Non-Homogeneous Differential Equations
In the above differential equation, if ![]() the linear differential equation is said to be homogeneous, and if
the linear differential equation is said to be homogeneous, and if ![]() is said to be non-homogeneous.
is said to be non-homogeneous.
2.3.3 The Standard Form of a Linear Differential Equation
A linear differential equation in the standard form will be as follows
(5) ![]()
2.3.4 The Solution of a Linear Differential Equation
The first step in solving such differential equations is to write it in the standard form. Then the integrating factor can be obtained as
(6) ![]()
The integration factor must be multiplied to both the left and right hand-side of the differential equation, which yields to
(7) ![]()
By integrating both sides of this equation, the solution to the linear differential equation will be obtained.
(8) ![]()
2.4 Exact Equations
2.4.1 The Definition of an Exact Equation
A first-order differential equation of the following form is said to be exact, if the left hand-side of the expression is an exact differential.
(9) ![]()
2.4.2 What is an exact differential?
The necessary and sufficient condition for the above differential equation to be an exact differential is
(10) ![]()
provided that
2.4.3 How to solve an exact equation?
For these type of equations, a function ![]() exists for which
exists for which
(11) ![]()
(12) ![]()
where
(13) ![]()
We assume that
(14) ![]()
By integrating this equation with respect to
2.5 Solution by Substitution
2.5.1 When to Use this Method?
A differential equation is usually solved by recognizing it as a certain kind of equation. Often the first step in solving a given differential equation consists of transforming it into another differential equation by means of substitution.
2.5.2 Homogeneous Function
If a function ![]() has a property of
has a property of
(15) ![]()
for some real number
2.5.3 Homogeneous Differential Equation
The following differential equation is said to be homogeneous if both coefficients ![]() and
and ![]() are homogeneous functions of the same degree.
are homogeneous functions of the same degree.
(16) ![]()
Either of the substitutions
2.5.4 Bernoulli’s Equation
The following differential equation is known as Bernoulli’s equation
(17) ![]()
where
2.5.5 Reduction to Separation of Variables
A differential equation of the form
(18) ![]()
can always be reduced to an equation with separable variables by means of the substitution
2.6 Linear Models
2.6.1 Growth and Decay
If we know the population at time ![]() , then we can find the population at any time
, then we can find the population at any time ![]() , where
, where ![]() , by solving the following initial-value differential equation.
, by solving the following initial-value differential equation.
(19) ![]()
where
2.6.2 Solution to the Growth and Decay Method as a Separable Equation
To solve this equation, as a separable DE, we need to first separate the variables,
(20) ![]()
then we need to integrate it, at find the constant of integration by using the initial condition.
(21) ![]()
(22) ![]()
So, the population at any given time,
(23) ![]()
2.6.3 Newton’s Law of Cooling/Warming
The mathematical formulation for cooling or warming a substance is given as a linear first-order differential equation. This equation is
(24) ![]()
where
2.7 Problems
- Find the critical points and phase portrait of the given autonomous first-order differential equation. Classify each critical point as asymptotically stable, unstable, or semi-stable.
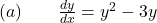
Answer: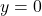 is an attractor and
is an attractor and 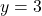 is a repeller. Watch the solution here.
is a repeller. Watch the solution here.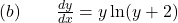
Answer: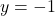 is an attractor and
is an attractor and 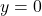 is a repeller. Watch the solution here.
is a repeller. Watch the solution here.
Answer: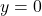 is an attractor and
is an attractor and 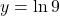 is a repeller. Watch the solution here.
is a repeller. Watch the solution here. - Solve the given differential equations by separation of variables.
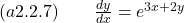
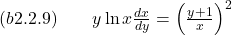
- Find an implicit and an explicit solution to the given initial value problem.
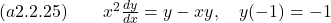
- Find the general solution of the given differential equation.
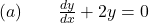
Answer: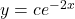 . Watch the solution here.
. Watch the solution here.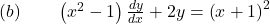
Answer: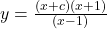 . Watch the solution here.
. Watch the solution here.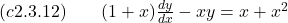
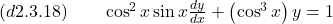
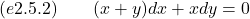

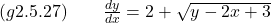
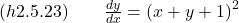
- Determine whether the given differential equation is exact. If it is exact, solve it.
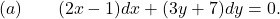
Answer: It is exact, and the solution is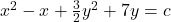 . Watch the solution here.
. Watch the solution here.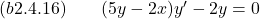
- Solve the given initial value problem.
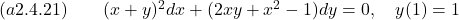
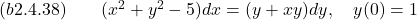
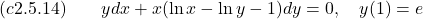
Reference
Dennis G. Zill. Advanced Engineering Mathematics, ![]() edition. Jones
edition. Jones ![]() Bartlett Learning. 2016.
Bartlett Learning. 2016.
