3.1 Theory of Linear Equations
3.1.1 What is an IVP?
For a linear differential equation, an ![]() -order Initial-Value Problem (IVP) is
-order Initial-Value Problem (IVP) is
(1) ![]()
which is solved using the given Initial-Value Conditions (IVC) as
(2) ![]()
3.1.2 What is a BVP?
For a linear differential equation, a second-order Boundary-Value Problem (BVP) is
(3) ![]()
which is solved using the Boundary Condition (BC) given at some points as
(4) ![]()
3.1.3 Linearly Dependent Functions
A set of functions are linearly dependent in an interval ![]() , if constants of
, if constants of ![]() exist in such a way that
exist in such a way that
(5) ![]()
for every
3.1.4 Criterion for Linearly Independent Solutions
A set of solutions of the homogeneous linear ![]() -order DE on an interval
-order DE on an interval ![]() are linearly independent if and only if the Wronskian of the solutions is non-zero.
are linearly independent if and only if the Wronskian of the solutions is non-zero.
3.1.5 Wronskian of a Set of Functions
The Wronskian of a set of functions is a determinant of a matrix and defined as follows, provided that all the functions have at least ![]() derivatives,
derivatives,
(6) 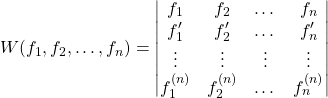
3.2 Reduction of Order
3.2.1 What is Reduction of Order method?
Suppose ![]() is a solution to the following homogeneous linear second-order differential equation.
is a solution to the following homogeneous linear second-order differential equation.
(7) ![]()
Recall that the solutions,
Now, by solving the first-order differential equation of
3.2.2 How does Reduction of Order work?
By dividing the homogeneous linear second-order differential equation by ![]() , we will recover the standard form as
, we will recover the standard form as
(8) ![]()
Suppose that
(9) ![]()
3.3 Homogeneous Linear Differential Equations with Constant Coefficients
3.3.1 Form an Auxiliary Equation
Consider the following second-order homogeneous linear differential equation with constant coefficients
(10) ![]()
Assume that the solution has the general form of
(11) ![]()
This equation will have the following two roots
(12) ![]()
3.3.2 Different Scenarios for the Auxiliary Equation
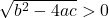 :
: 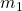 and
and 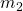 are real and distinct
are real and distinct 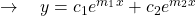 .
.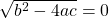 :
: 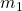 and
and 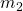 are real and equal
are real and equal 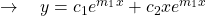 .
. :
: 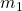 and
and 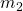 are conjugate complex numbers, and
are conjugate complex numbers, and 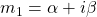 and
and 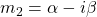 . Then,
. Then, 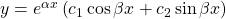 .
.
3.3.3 Higher-Order Equations
Consider the following high-order homogeneous linear differential equation with constant coefficients
(13) ![]()
the auxiliary equation will be an
(14) ![]()
The solution to the differential equation depends on the roots of the auxiliary equation and is determined similarly to the previous section.
3.4 Non-Homogeneous Linear Differential Equations
A non-homogeneous linear differential equation has a general form of
(15) ![]()
We need to find the complementary function,
(16) ![]()
The complementary function is found using the methods that we learnt so far; however, there are different methods to find the particular solutions.
3.4.1 Method of Undetermined Coefficients
The idea of this method is an educated guess about the form of ![]() based on the input function
based on the input function ![]() . This method is only suitable if the coefficients,
. This method is only suitable if the coefficients, ![]() , are constants, and
, are constants, and ![]() is a constant, a polynomial function, an exponential function
is a constant, a polynomial function, an exponential function ![]() , sine or cosine functions
, sine or cosine functions ![]() or
or ![]() , or finite sums and products of these functions.
, or finite sums and products of these functions.
The following functions are some examples of the types of inputs ![]() that are appropriate:
that are appropriate:
![]()
![]()
![]()
![]()
![]()
And here are some examples of the types of inputs
![]()
![]()
![]()
![]()
To find a particular solution to a non-homogeneous linear differential equation using the method of undetermined coefficients, we first need to assume a form of ![]() based on
based on ![]() and then substitute
and then substitute ![]() in the differential equation to find the coefficients.
in the differential equation to find the coefficients.
Note that if any ![]() contains terms that duplicate terms in
contains terms that duplicate terms in ![]() , then that
, then that ![]() must be multiplied by
must be multiplied by ![]() , where
, where ![]() is the smallest positive integer that eliminates that duplication.
is the smallest positive integer that eliminates that duplication.
3.4.2 Method of Variation of Parameters
First, we need to write the linear second-order differential equation in the standard form,
(17) ![]()
Then, the particular solution is
(18) ![]()
(19) ![]()
And, for higher-order non-homogeneous differential equations of the form
(20) ![]()
we have
(21) ![]()
3.5 Cauchy-Euler Differential Equations
The Cauchy-Euler equation, Euler-Cauchy equation, Euler equation, or equidimensional equation, is any linear differential equation of the form
(22) ![]()
where the coefficients
To find the complementary function, i.e. the solution to the associated homogeneous differential equation, we assume that the solution has a general form of
3.5.1 Second-Order Cauchy-Euler Differential Equation
The homogeneous second-order linear Cauchy-Euler differential equation has a general form of
(23) ![]()
The auxiliary equation is
(24) ![]()
Based on the roots of the auxiliary equation, there will be three different solutions to the given ordinary differential equation.
- Distinct Real Roots.
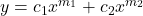 .
. - Repeated Real Roots.
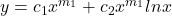 .
. - Conjugate Complex Roots.
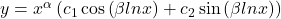 .
.
3.6 High-Order Linear Differential Equations with Variable Coefficients
3.6.1 Power Series Solution
Whenever the coefficients of a high-order differential equation are variable, we assume that the solution has a form of power series. The solution and its derivatives will have the following form
(25) ![]()
(26) ![]()
(27) ![]()
![]()
Then, we will substitute the above derivatives in the original differential equation and shift the summation index so that all of the power series are of degree
3.7 Problems
Reference
Dennis G. Zill. Advanced Engineering Mathematics, ![]() edition. Jones
edition. Jones ![]() Bartlett Learning. 2016.
Bartlett Learning. 2016.
