Chapter 4 – Functions of Complex Variables

4.1 Complex Number

4.1.1 Definition

Any number of the form z = a + i b is called a complex number, where a and b are real numbers and i is the imaginary unit.
The real part of the complex number, z, is x, and y is the imaginary part of z.

4.1.2 Arithmetic Operations

Addition

(1)   \begin{equation*}z_1 + z_2 = (x_1 + i y_1) + (x_2 + i y_2) = (x_1 + x_2) + i (y_1 + y_2) .\end{equation*}


Subtraction

(2)   \begin{equation*}z_1 - z_2 = (x_1 + i y_1) - (x_2 + i y_2) = (x_1 - x_2) + i (y_1 - y_2) .\end{equation*}


Multiplication

(3)   \begin{equation*}z_1 z_2 = (x_1 + i y_1) (x_2 + i y_2) = x_1x_2 - y_1y_2 + i ( y_1x_2 + x_1y_2 ) .\end{equation*}


Division

(4)   \begin{equation*}\frac{z_1}{z_2} = \frac{x_1 + i y_1}{x_2 + i y_2} = \frac{x_1 x_2 + y_1 y_2}{x_2^2 + y_2^2} + i \frac{y_1 x_2 - x_1 y_2}{x_2^2 + y_2^2} .\end{equation*}

4.1.3 Conjugate

If z = x + i y is a complex number, then the complex conjugate, or simply the conjugate, of z is

(5)   \begin{equation*}\overline{z} = x - i y .\end{equation*}


The arithmetic operations of a conjugate are as follows

(6)   \begin{equation*}\overline{z_1 + z_2} = \overline{z_1} + \overline{z_2}, \quad \quad \overline{z_1 - z_2} = \overline{z_1} - \overline{z_2}, \quad \quad \overline{z_1 ~ z_2} = \overline{z_1} ~ \overline{z_2}, \quad \quad \overline{\left( \frac{z_1}{z_2} \right)} = \frac{\overline{z_1}}{\overline{z_2}}.\end{equation*}

4.1.4 Modulus or Absolute Value

The absolute value of z = x + i y is defined as

(7)   \begin{equation*}\left| z \right| = \sqrt{x^2 + y^2} = \sqrt{z \overline{z}} .\end{equation*}

4.1.5 Geometric Interpretation

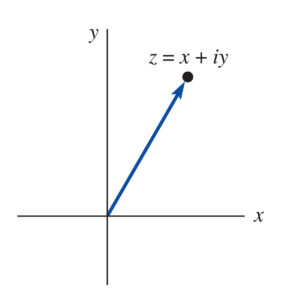
The following coordinate plane is known as the complex plane or simply the z-plane. The x-axis is the real axis, and the y-axis is the imaginary axis. The absolute value of a complex number is the distance of that number to the origin.

4.2 Powers and Roots

4.2.1 Polar Form

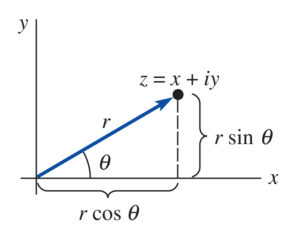
The polar form of a complex number, z = x+iy, is

(8)   \begin{equation*}z = (r \cos \theta) + i (r \sin \theta) = r ( \cos \theta + i \sin \theta ) .\end{equation*}

4.2.2 DeMoivre’s Formula

(9)   \begin{equation*}\left( \cos \theta + i \sin \theta \right)^n = \cos n \theta + i \sin n \theta .\end{equation*}

4.2.3 Integers Powers of z

The integer powers of a complex number can be found easily by applying the DeMoivre’s formula on the polar form of z as follows

(10)   \begin{equation*}z ^ n = \left( r \cos \theta + i ~ r \sin \theta \right)^n ,\end{equation*}


(11)   \begin{equation*}z ^ n = r^n \left( \cos \theta + i \sin \theta \right)^n ,\end{equation*}


(12)   \begin{equation*}z ^ n = r^n \left( \cos n \theta + i \sin n \theta \right) .\end{equation*}

4.2.4 Roots of z

A number w is the n^{th} root of a complex number z, if w^n = z.
Let’s assume that w = \rho \left( \cos \phi + i \sin \phi \right), then we can find the values of \rho and \phi as follows

(13)   \begin{equation*}w ^ n = z ,\end{equation*}


(14)   \begin{equation*}\rho^n (\cos n \phi + i \sin n \phi ) = r (\cos \theta + i \sin \theta) .\end{equation*}


So, \rho = r ^ {\frac{1}{n}}, and

(15)   \begin{equation*}\Big( \cos n \phi = \cos \theta \quad \& \quad \sin n \phi = \sin \theta \Big) \quad \Rightarrow \quad n \phi = \theta + 2 k \pi .\end{equation*}


By summarizing the results, the n^{th} roots of a given non-zero complex number are

(16)   \begin{equation*}w_k = r^{\frac{1}{n}} \left[ \cos \left( \frac{\theta + 2 k \pi}{n} \right) + i \sin \left( \frac{\theta + 2 k \pi}{n} \right) \right] .\end{equation*}

4.3 Problems

Reference

Dennis G. Zill. Advanced Engineering Mathematics, 6^{th} edition. Jones & Bartlett Learning. 2016.