1.1 What is a Differential Equation?
Differential Equation (DE) is an equation which contains the derivatives of one or more dependent variables with respect to one or more independet variables.
1.2 ODE vs PDE
Ordinary Differential Equation (ODE): A differential equation that contains the derivative of one or more dependent variables, with respect to only one independent variable. Example of an ODE:
(1) ![]()
where
Partial Differential Equation (PDE): A differential equation that contains the derivative of one or more dependent variables, with respect to more than one independent variables. Example of a PDE:
(2) ![]()
where
1.3 The Order of a DE
The order of a differential equation is the order of the highest derivative in the equation. A second-order PDE and a third-order ODE are shown below.
(3) ![]()
1.4 Different Forms of a DE
An ![]() th order DE, with
th order DE, with ![]() as its independent variable and
as its independent variable and ![]() as its dependent variable, can be expressed in the general form as:
as its dependent variable, can be expressed in the general form as:
(4) ![]()
and in the normal form as:
(5) ![]()
1.5 Linear vs Non-Linear ODE
An ![]() th order DE is linear in the variable
th order DE is linear in the variable ![]() if
if ![]() be linear in
be linear in ![]() and all its derivatives. Being linear in a
and all its derivatives. Being linear in a ![]() means that the degree of
means that the degree of ![]() and all its derivatives must be one, and their coefficients cannot be a function of
and all its derivatives must be one, and their coefficients cannot be a function of ![]() or its derivatives. A non-linear DE is simply one that is not linear. More examples for clarification:
or its derivatives. A non-linear DE is simply one that is not linear. More examples for clarification:
1.6 Explicit and Implicit Solutions
A solution in which the dependent variable is expressed solely in terms of the independent variable and constants is said to be an explicit solution.
1.7 Families of Solutions
When solving an n![]() -order differential equation,
-order differential equation, ![]() , we seek an n-parameter family of solutions
, we seek an n-parameter family of solutions ![]() . For example, the one-parameter family
. For example, the one-parameter family ![]() is an explicit solution of the linear first-order equation
is an explicit solution of the linear first-order equation ![]() .
.
1.8 Initial-Value Problems
We are often interested in problems in which we seek a solution ![]() of a differential equation so that
of a differential equation so that ![]() satisfies prescribed side conditions – that is, conditions that are imposed on the unknown
satisfies prescribed side conditions – that is, conditions that are imposed on the unknown ![]() or on its derivatives.
or on its derivatives.
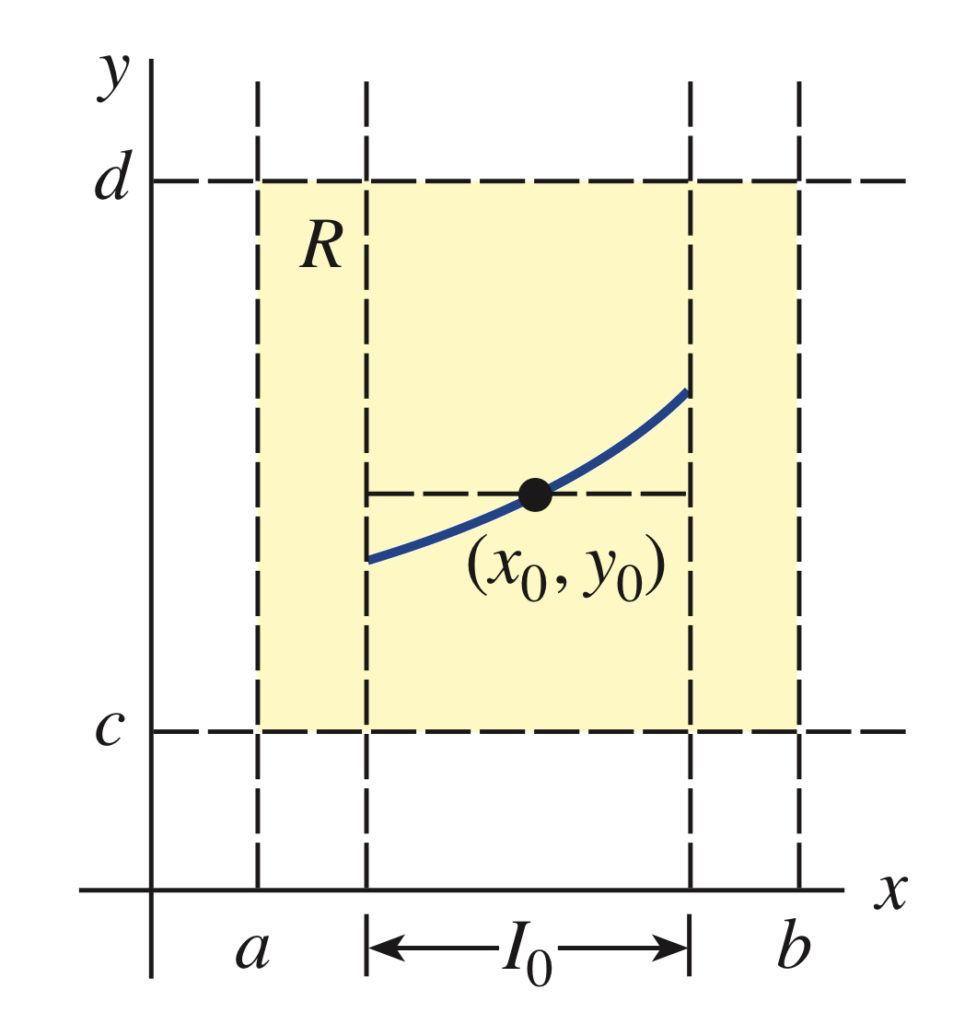
1.9 Existence of a Unique Solution
Let ![]() be a rectangular region in the
be a rectangular region in the ![]() -plane defined by
-plane defined by ![]() , that contains the point
, that contains the point ![]() in its interior. If
in its interior. If ![]() and
and ![]() are continuous on
are continuous on ![]() , then there exists some interval
, then there exists some interval ![]() , contained in
, contained in ![]() , and a unique function
, and a unique function ![]() defined on
defined on ![]() that is a solution of the initial-value problem.
that is a solution of the initial-value problem.
1.10 A 10-minute Lecture on the Basic Terminology of Differential Equations
1.11 Problems
- State the order of the given differential equations and determine whether it is linear or non-linear.
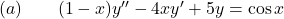
Answer: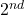 -Order Linear Differential Equation. Watch the solution here.
-Order Linear Differential Equation. Watch the solution here.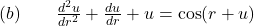
Answer: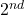 -Order Non-Linear Differential Equation. Watch the solution here.
-Order Non-Linear Differential Equation. Watch the solution here.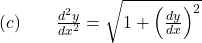
Answer: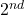 -Order Non-Linear Differential Equation. Watch the solution here.
-Order Non-Linear Differential Equation. Watch the solution here.
Reference
Dennis G. Zill. Advanced Engineering Mathematics, ![]() edition. Jones
edition. Jones ![]() Bartlett Learning. 2016.
Bartlett Learning. 2016.
