Why Do We Need Stabilization?
High-order flux reconstruction schemes are more sensitive to numerical instabilities due to their relatively low numerical dissipation. These numerical instabilities are mainly arised from the non-linearity of Navier-Stokes equations. The instabilities can be dealt with using different techniques:
– Choosing a good set of solution points,
– Anti-Aliasing,
– Limiters,
– Artificial Dissipation,
– Filtering.
Set of Solution Points. Based on Runge’s phenomena, equidistant points are a poor choice having spurious oscillations at the edges of an interval. To alleviate this, a set of points should be chosen that are biased towards the ends of the domain, i.e. Gauss points.
Anti-Aliasing. Aliasing occurs when a higher degree polynomial is projected to a lower one. This is usually of high concern in non-linear equations. In the Navier-Stokes equations, the flux is a non-linear function of the conserved quantities, therefore aliasing arises in the projection of the flux polynomial onto the space of the solution polynomial. Anti-aliasing does remove the aliasing instabilities but at a significant computational cost.
Limiters. The limiting technique is often used for problems containing shocks and strong discontinuities. The limiter essentially reconstructs the solution to reduce its oscillatory behavior, using information from neighboring elements. This technique destroys the local accuracy in the limited cells.
Artificial Viscosity. This technique needs a detector to add artificial viscosity as required to the troubled cells, which smears small-scale structures such as vortices.
Filtering. The filtering method is investigated and implemented for large eddy simulation. The accuracy of the filtering technique has always been questioned. However, optimized filters are introduced in this research that is capable of stabilizing the simulation while maintaining the order of accuracy.
Simulations Using the Optimized Filters
The details of these simulations can be found in the published paper and/or the published thesis.
Isentropic Vortex. The advection of an isentropic vortex with the mean flow is simulated using Euler equation in the in-house solver at Computational Aerodynamics Lab.
The Taylor-Green Vortex. The suitability of the proposed filters for large eddy simulation is studied by solving the Navier-Stokes equations using the Taylor-Green Vortex. The flux reconstruction approach developed in an in-house solver in Computational Aerodynamics Lab is used for this simulation. The filtered and non-filtered simulations are shown below.
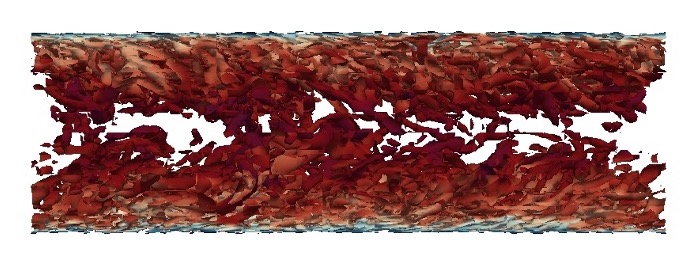
The Turbulent Channel. Fully-developed turbulent channel flow is studied as validation for wall-bounded turbulent flows. The developed in-house solver in Computational Aerodynamics Lab is used for this simulation. Different polynomial degrees are used for this simulation and the isosurface of Q-criterion colored by velocity is shown for the filtered ![]() simulation.
simulation.
The NACA0020 Airfoil. Flow over a NACA0020 airfoil at a high angle of attack is simulated. The developed in-house solver in Computational Aerodynamics Lab is used for this simulation. The isosurface of Q-criterion colored by velocity is shown for the filtered and non-filtered ![]() simulation.
simulation.


